大开眼界,“一网打尽”数学中,所有“最”重要的定理和难题
数学中有成千上万的定理与猜想,但只有少数几个被视为根本而基本的。有些已经被证明,另一些仍在等待它们的解答。让我们来看看其中有哪些。

巴拿赫-塔尔斯基悖论
巴拿赫-塔尔斯基悖论声称,在三维空间中,一个实心球可以被分割成有限个互不重叠的部分,然后仅通过旋转和平移,就能重新组合成两个与原球完全相同的球体。当然,这一悖论背后涉及大量数学内容,但这就是它的核心。
这一悖论已被数学证明成立,但它依赖于选择公理。所涉及的那些部分是高度不可构造的,它们碎裂得如此极端,以至于无法明确描述,亦无法在物理上实现。
三体问题
三体问题提出的问题是:已知三个天体的初始位置和速度,它们在彼此的万有引力作用下将如何运动?
这个问题说起来简单,解起来却极其复杂。一般而言,牛顿定律给出了物体在引力作用下相互影响的精确方程。对于两个物体,我们会得到椭圆轨道。但一旦引入第三个物体,情况就变得混乱得多。它们的轨迹可能彼此缠绕、交换能量,并在长期行为上变得无法用公式预测。
庞加莱在19世纪90年代证明,这个问题没有一般性的解析解,也就是说不存在简单公式来描述所有解。这是后来被称为混沌理论的最早迹象之一。三体系统的运动对初始条件极其敏感。
ABC猜想
ABC猜想于1985年提出。粗略地说,它指出:如果三个整数 a、b、c 满足 a + b = c,且这三个数彼此之间没有任何公因子,同时每个数含有很多重复的质因数,那么 c 通常不会比所有出现在 a、b、c 中的质数的乘积大太多。
这个质数乘积被称为 ABC 的“根”(radical)。所谓 radical,就是将所有不重复的质因数相乘,不考虑它们的指数。例如:
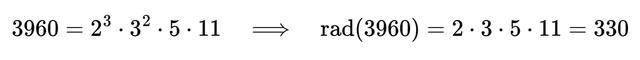
猜想表述为:
若 a + b = c,且 a、b、c 两两互素,那么
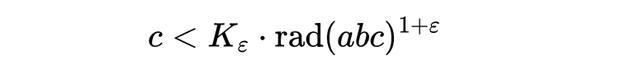
其中 Kε 是与 ε 相关的常数
这个猜想可以解释为何像 xⁿ + yⁿ = zⁿ 这类方程几乎没有所有数互素的整数解。
尽管有一位名叫望月新一(Shinichi Mochizuki)的数学家声称他已用一种他称为“宇宙际泰克理论”(Inter-universal Teichmüller Theory)的复杂理论证明了 ABC 猜想,但这一成果至今仍未获得广泛验证,甚至难以被同行理解。
阿蒂亚–辛格指数定理
这个定理关注的是椭圆型线性偏微分方程的解的存在性与唯一性。
来看两个非常相似的方程:
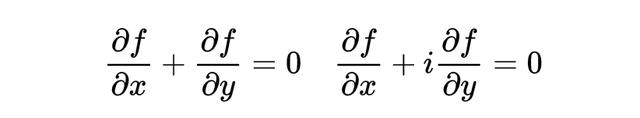
它们之间只差一个 i系数,却有完全不同的行为。
第一个方程:任何形如 f(x, y) = g(x − y) 的函数都是其解;
而第二个方程,仅有常数且有界的函数才是其解,这是由刘维尔定理(Liouville’s Theorem)所决定的。
这种差异来自方程的“符号函数”(symbol),符号函数是将偏导数形式中的导数符号用变量(例如 iξ 与 iη)替换后得到的多项式。
这两个方程的符号函数分别为:iξ + iη 与 iξ − η。
一个偏微分方程被称为“椭圆型”的条件是:其符号函数仅在所有变量都为零时才为零。换句话说,即符号函数的零点是唯一的原点。
伯奇–斯温纳顿-戴尔猜想(Birch–Swinnerton-Dyer 猜想)
这个猜想试图揭示某类方程的有理数解的数量,这类方程被称为椭圆曲线。问题是:某条椭圆曲线有多少个有理解,也就是分数或整数解?
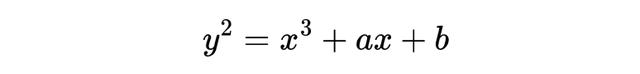
猜想指出,这个数量与该椭圆曲线的 L-函数之间有深刻联系,这个函数的形式如下:
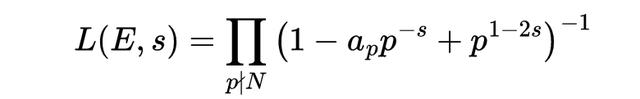
比如考虑方程:y² = x³ − x
这条曲线有无限多个有理数解。按照该猜想,这是因为 L-函数在某个关键点 s = 1 处为零。
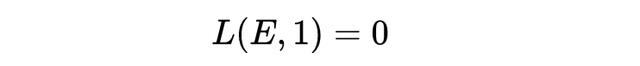
换句话说,L-函数在 s = 1 处为零,是该曲线拥有如此多有理解的猜想性原因。
尽管这一猜想有大量证据支持,但仍未被证明,因此成为七个“千禧年难题”之一。任何人只要证明它,就能获得一百万美元的奖金。
卡尔松定理(Carleson’s Theorem)
卡尔松定理回答了一个关于傅里叶级数的基本问题——傅里叶级数是一种将函数表示为正弦与余弦波之和的方法。问题是:如果一个函数是平方可积的(也就是说,它属于 L² 空间),那么它的傅里叶级数是否几乎处处都收敛于原函数?
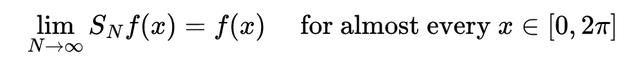
这个问题悬而未解将近一个世纪,直到1966年被证明:是的,任何 L² 函数的傅里叶级数几乎处处都收敛于它自身。
最终的结论是:尽管会出现吉布斯现象(Gibbs overshoot)和其他复杂性,这些傅里叶近似仍然在“几乎处处”的意义下点态收敛。
柯西定理(Cauchy’s Theorem)
复分析中的柯西定理指出:如果一个函数在某个闭合曲线内部及其上都是复可微的(也就是全纯的),那么这个函数沿着该闭合曲线的积分为零。
中心极限定理(Central Limit Theorem)
这个定理指出:如果我们取一列独立同分布的随机变量,且它们的均值 μ 和方差 σ² 都是有限的,那么这些变量的标准化和,会随着样本数 n 趋近无穷,收敛于标准正态分布。
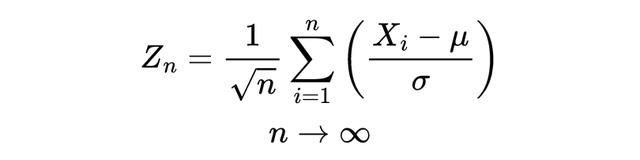
换句话说:即使原始数据不呈现钟形分布,但只要样本数量足够大,它们的和或平均值最终会趋近于钟形分布。
有限单群的分类定理(The Classification of Finite Simple Groups)
这个分类定理属于群论领域,它完成了对所有有限单群的分类。有限单群被认为是所有有限群的“构件单元”,就像质数之于整数。
定理指出:所有有限单群都属于以下四类之一:
素阶循环群(cyclic groups of prime order)交错群(alternating groups)李型群(groups of Lie type)以及 26 个特殊的例外群,被称为“零星群”(sporadic groups)这项证明工程庞大,耗时数十年,动员了数百位数学家,总计撰写了数万页的论文。
狄利克雷定理(Dirichlet’s Theorem)
狄利克雷在19世纪证明的算术级数定理指出:若正整数 a 与 d 互素,则算术序列 a, a+d, a+2d,... 中包含无穷多个质数。
遍历定理(Ergodic Theorems)
这些定理在20世纪初发展起来,研究的是动力系统的长期行为。基本思想是:观察一个系统随时间演化的轨迹(例如箱子中气体分子的运动),与在某一固定时刻对系统所有可能状态的平均进行比较,在特定条件下,两种平均值是相等的。
费马大定理(Fermat’s Last Theorem)
费马大定理断言:不存在满足 xⁿ + yⁿ = zⁿ 的正整数解,当整数 n 大于 2 时。
虽然费马声称自己找到了这个定理的证明,但他的书信和笔记中都未曾留下证据。这一问题悬而未决达350年,直到1994年,安德鲁·怀尔斯(Andrew Wiles)借助远远超出费马时代的数学工具才得以证明这一命题。
不动点定理(Fixed Point Theorems)
这些定理声称:在某些条件下,一个函数总会有至少一个“不动点”,即映射后仍在原处的点。
最著名的版本是布劳威尔不动点定理(Brouwer's Fixed Point Theorem),它指出:任何从一个封闭圆盘(或球体)映射到自身的连续函数,都至少有一个不动点。
比如你搅动一杯咖啡,总有一滴液体会回到它原来的位置。
四色定理(Four Color Theorem)
该定理断言:在一个平面上或球面上绘制的任意地图,最多只需要四种颜色就能进行着色,使得没有两个相邻区域具有相同的颜色。
四色问题最初是在19世纪提出的,但令人意外的是,它长时间未能被证明。
直到1976年,肯尼斯·阿佩尔(Kenneth Appel)与沃尔夫冈·哈肯(Wolfgang Haken)首次利用计算机辅助方法完成了它的证明。由于需要检查超过一千种特殊情况,计算机成为不可或缺的工具。这也是历史上首批必须依赖计算机验证的数学定理之一。
代数学基本定理(Fundamental Theorem of Algebra)
该定理表明:任意一个次数为 n 的多项式方程在复数域中都有恰好 n 个复根。
例如,考虑简单的多项式 z² + 1:它在实数域中没有解,但在复数域中有两个解:±i。
这表明,为了解多项式方程,我们无需超越复数的范畴,复数域已经“完备”。
算术基本定理(Fundamental Theorem of Arithmetic)
该定理指出:除了 1 以外的每个正整数都能唯一地分解为若干个质数的乘积。唯一性仅体现在质因数的组合,不考虑它们出现的顺序。
微积分基本定理(Fundamental Theorem of Calculus)
简要来说,该定理揭示了积分与微分之间互为逆过程的关系。
更精确地说,对于某函数 f(x),其在区间 [a, b] 上的定积分,等于该函数一个原函数在 b 与 a 处的差值:
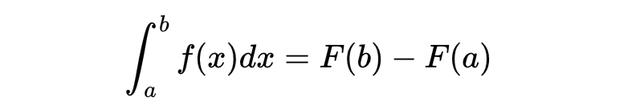
其中 F(x) 是 f(x) 的一个原函数。
哥德尔不完全性定理(Gödel’s Incompleteness Theorem)
哥德尔的第一不完全性定理指出:在任何一个一致且足够强大,能表达基本算术的形式系统中,总存在一些命题,它们在该系统内既无法被证明,也无法被否定。
哥德巴赫猜想(Goldbach Conjecture)
这是数论中最古老的未解问题之一。它提出:每个大于 2 的偶数都可以写成两个质数之和。
尽管迄今为止没人找到反例,计算机也已验证了极大的数值范围,但该猜想至今仍无通用性证明。
格罗莫夫多项式增长定理(Gromov’s Polynomial Growth Theorem)
该定理断言:如果一个群的增长是多项式型的——即用至多 n 个生成元所能生成的元素数量随 n 增长为一个多项式函数——那么这个群是“几乎幂零”的(virtually nilpotent)。
许多群(如自由群)的增长是指数级的,而本定理界定了多项式增长群的结构。
希尔伯特零点定理(Hilbert’s Nullstellensatz)
在德语中意为“零点集合定理”。该定理指出:如果一组多项式有共同的零点,那么这些零点构成一个代数簇,即某个理想的零点集。
换言之,在某个理想中进行多项式组合(如 f + g)不会改变函数消失的点集,它们仍属于同一零点集合。
连续统假设的独立性(Independence of the Continuum Hypothesis)
连续统假设问:是否存在某个集合,其基数大小严格介于自然数集的基数与实数集的基数之间?
至今没人知道答案是什么。哥德尔与科恩分别证明了它在 ZFC 公理体系下既无法被证明,也无法被否定,因此该命题是独立的。
不等式(Inequalities)
数学中一些最重要且经常使用的不等式包括柯西-施瓦茨不等式(Cauchy–Schwarz)、赫尔德不等式(Hölder)、詹森不等式(Jensen),以及切比雪夫不等式(Chebyshev)。
它们的主要作用是在无法计算精确答案时,用于估计或界定值域范围。
停机问题的不可解性(Insolubility of the Halting Problem)
停机问题问:是否存在一个通用算法,能够判断任意计算机程序和任意输入,在该输入下程序是否最终会停止运行?
艾伦·图灵于1936年证明:这样的算法不存在。换句话说,这个问题是不可判定的,即不存在有限一致的方法能在所有情形下正确地回答这个问题。
五次方程不可解性(Insolubility of the Quintic)
一元二次、三次、四次多项式都有通用求根公式,但五次及更高次的多项式不存在用根式(radicals)表示通解的普遍公式。
19世纪,鲁菲尼(Ruffini)、阿贝尔(Abel)与伽罗瓦(Galois)等人证明:一般五次方程无法用根式解。这一成果也推动了伽罗瓦理论的诞生。
刘维尔定理与罗斯定理(Liouville's Theorem and Roth’s Theorem)
刘维尔定理表明:某些数无法被有理数很好地逼近。具体而言,如果 α 是一个代数数,其次数 d ≥ 2,那么存在一个常数 c > 0,使得对于所有有理数 p/q,下面这个不等式总成立:
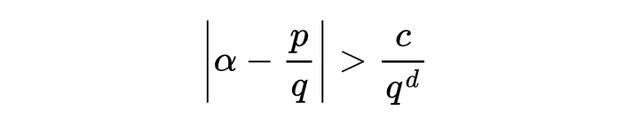
这一定理给出了首批超越数的构造方法。
而罗斯(Klaus Roth)则在此基础上进一步推进。他证明:对于任意代数有理数 α,任意 ε > 0,只有有限多个有理数 p/q 满足:
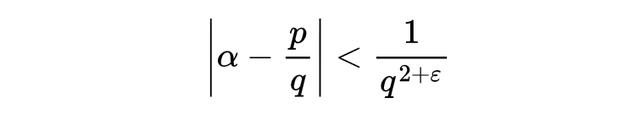
这说明代数数无法被有理数“太好地”逼近。罗斯定理在理论上达到了这个问题的最优结果,也因此他获得了菲尔兹奖。
(简言之,代数数总是“回避”被非常精确的分数近似。)
莫斯托强刚性定理(Mostow's Strong Rigidity Theorem)
该定理指出,在维数大于2的情形下,一个空间的几何结构是由其基本群(fundamental group)完全决定的,至少在负曲率空间(如双曲流形)中是如此。
更准确地说:如果两个紧致的 n 维双曲流形(n ≥ 3)有同构的基本群,那么它们是等距的——也就是说,它们之间存在一个保持距离不变的映射。
这一点相当令人惊讶,因为在二维情况下,例如黎曼曲面中,即便拓扑结构相同,仍可拥有许多不同的几何结构(也就是模空间非常丰富)。但在三维及以上维度中,这种灵活性突然“刚性化”了。
P = NP 问题(The P vs NP Problem)
P vs NP 问题探讨的是:所有可以在多项式时间内验证其解的计算问题,是否也能在多项式时间内求解?核心问题是:验证一个答案是否比找到这个答案更容易吗?换句话说,是否 P = NP?
这是理论计算机科学与数学中最重要的未解难题之一,目前尚无解答。
庞加莱猜想(Poincaré Conjecture)
简单来说:如果一个三维空间没有“洞”,而空间中的每个闭合环都可以连续收缩成一点,那么这个空间就与三维球面本质相同。
更正式的说法是:任何封闭的、三维的、单连通流形都同胚于三维球面 S³。
庞加莱在1904年提出了这个猜想,它成为数学界最著名的难题之一,长时间未解。
直到2003年,格里高利·佩雷尔曼(Grigori Perelman)运用理查德·汉密尔顿(Richard Hamilton)提出的 Ricci 流(Ricci flow)方法,终于完成了证明。佩雷尔曼因其成就获得了菲尔兹奖和“千禧年大奖”,但他拒绝了这两个奖项。
素数定理与黎曼猜想(The Prime Number Theorem and the Riemann Hypothesis)
我们可以问:1 到 n 之间有多少个质数?
最自然的做法是定义 π(n) 为不超过 n 的质数个数,然后寻找一个表达 π(n) 的公式。但众所周知,质数并无明显规律,甚至我们都不确定是否存在这样的精确公式。
数学家采取的标准策略是寻找良好的“估计”。素数定理就提供了这样一个估计:当 n 趋近无穷大时,π(n) 近似于 n / ln(n)。
这表明,虽然质数随着数字增大而变得稀疏,但这种变稀是有规律的,并且受对数函数的精确控制。
这又引出了一个更深的问题:这个估计有多精确?
这就涉及到了黎曼猜想(Riemann Hypothesis):猜想中指出,黎曼ζ函数(Zeta function)的所有“非平凡零点”都位于复平面上实部为 1/2 的垂直线上。
如果这个猜想被证明,它将为素数定理中的误差项提供严格界限。这也是数学中最重要的未解难题之一。
加法数论中的问题与结果(Problems and Results in Additive Number Theory)
以下是数论中三个著名的未解问题:
是否每个大于 4 的偶数都能写成两个奇质数之和?(即哥德巴赫猜想)是否存在无穷多个孪生质数对(即差为 2 的质数对)?(即孪生素数猜想)是否每个足够大的正整数都可以写成四个立方数的和?(即沃林问题的一个特例)这些问题至今悬而未解,是加法数论领域中最引人瞩目的难题。
从二次互反律到类域论(From Quadratic Reciprocity to Class Field Theory)
高斯发现的二次互反律(Law of Quadratic Reciprocity)是数论中最早的深刻定律之一。它揭示了一个对称性的关系:我们可以通过比较两个质数 p 和 q,来判断关于模 p 的一个二次同余方程是否在 q 下有解,反之亦然。
换句话说:判断方程 x^2≡ p mod q是否有解,可以转化为判断另一个看似无关的问题。这种对称性令人惊奇。
数学家们随后探索了更高次数的同余方程,发现类似的规律依旧存在,但变得更加复杂且抽象。这最终引向了类域论(Class Field Theory)的诞生——这是研究阿贝尔扩张(也就是交换性的数域扩张)的一门理论。
类域论的核心观点是:不再用单个数来表达互反律,而是引入了“理想类”(ideal classes)与“伽罗瓦群”(Galois groups)来揭示数域扩张之间的结构性规律。
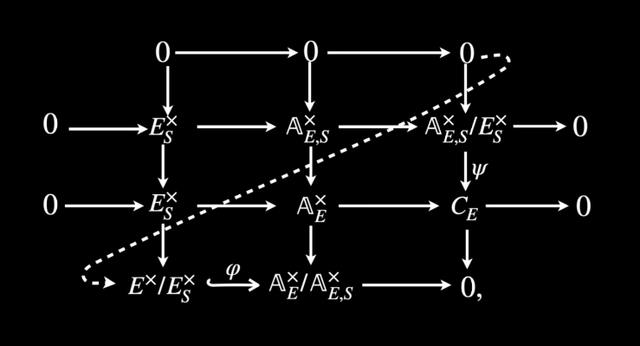
类域论是现代代数数论的基石之一,它将早期的局部规律整合为一种全局的对称结构。
代数曲线上的有理点与莫迪尔猜想(Rational Points on Curves and the Mordell Conjecture)
在研究二元多项式方程的解时,我们通常将其视为定义了一条“曲线”。一个核心问题是:这样一条曲线上有多少个“有理点”,即 x 与 y 都为有理数的解?

答案强烈依赖于曲线的“亏格”(genus),也就是它的复杂程度,比如它有多少个“洞”:
亏格为 0 的曲线要么没有有理点,要么有无穷多个;亏格为 1 的曲线(例如椭圆曲线)上的有理点组成一个有限生成的阿贝尔群;当亏格大于等于 2 时,情况就截然不同:曲线上仅存在有限多个有理点。这个结果就是著名的莫迪尔猜想(Mordell Conjecture),后由法尔廷斯(Faltings)在1983年成功证明,是现代代数几何与数论融合的重要成果。
奇点解析(The Resolution of Singularities)
在代数几何中,一个奇点是指某个代数簇上的“异常点”——即该点处不光滑,可能有尖点、自交点等。
“解析奇点”指的是通过一系列几何操作,将含有奇点的对象转化为光滑对象的过程。
主定理指出:对于特征为零的域(如实数域或复数域)上的任意代数簇,都存在一个奇点解析,也就是说,可以通过代数几何中的合法手段将其平滑化。这是现代代数几何中的基础工具之一。
黎曼–罗赫定理(The Riemann–Roch Theorem)
该定理告诉我们,在一条曲线上,具有给定零点与极点(即除法器)的亚纯函数(meromorphic function)的数量,可以仅凭这条曲线的亏格(genus)和除法器的次数(degree)来计算。
这个定理将函数的存在性与拓扑结构(如亏格)之间建立了深刻联系,是代数几何的核心支柱之一。
罗伯逊–西摩尔定理(The Robertson–Seymour Theorem)
该定理指出:在所有有限图的集合中,图在“图的子图-删边-缩边”的意义下是良序的(well-quasi-ordered)。
通俗地说,在任何一个无限的图序列中,总可以找到一个图是序列中某个更晚图的“次图”或“图的次结构”。
这个结果在结构图论和算法理论中具有深远意义,是图论中最深刻的成果之一。
瑟斯顿几何化猜想(Thurston’s Geometrization Conjecture)
瑟斯顿提出,这个世界上每一个封闭的三维流形都可以分解成若干块,每一块都携带着一种来自八种可能几何结构之一的“标准形态”。
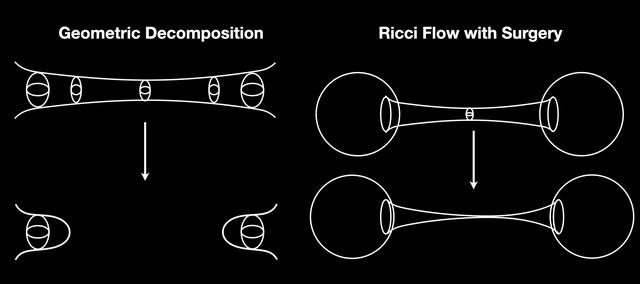
这就像是在说:尽管三维空间可能被扭曲得很复杂,但每一部分都在某种“标准模板”的范畴内。
这一猜想后来由佩雷尔曼在解决庞加莱猜想的过程中一并完成,因此瑟斯顿猜想也因此被视为“已经被证明”。
一致化定理(The Uniformization Theorem)
一致化定理指出:每一个单连通的黎曼曲面,在共形等价(即保持角度结构的变换)意义下,必与以下三者之一完全等价:
单位圆盘(Poincaré圆盘)复平面黎曼球面这是黎曼面分类与复几何基础中的核心定理之一。
韦尔猜想(The Weil Conjectures)
这是最难以简要总结的一部分,但我尽力:
1940年代,安德烈·韦尔(André Weil)提出了一组猜想,它们旨在揭示有限域上代数簇的点数与其几何性质之间的深刻联系。
具体地说,对于定义在有限域上的代数簇 V,我们构造出它的 ζ-函数:
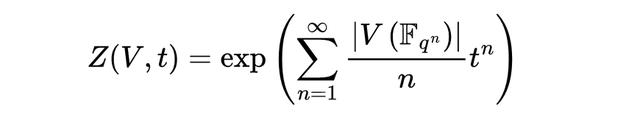
韦尔猜测该函数具有以下四个性质:
有理性:ζ-函数是有理函数;对称性:它满足形如的对称关系,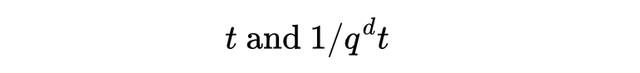 因式分解:ζ-函数可以写成若干个与贝蒂数相关的多项式乘积;零点与极点的位置:这些点都位于特定的“临界直线”上,类似于复ζ函数的黎曼猜想。
因式分解:ζ-函数可以写成若干个与贝蒂数相关的多项式乘积;零点与极点的位置:这些点都位于特定的“临界直线”上,类似于复ζ函数的黎曼猜想。这些猜想在几十年内陆续被证明,它们推动了现代同调理论与代数几何的深远发展。德利涅(Deligne)在1970年代完成了最深刻部分的证明,成为代数几何里程碑式的胜利。
大家都在看
-
为啥说社会主义制度最科学?这三个日常细节,戳中每个普通人! 提起“社会主义制度”,可能有人觉得太抽象,其实它藏在咱们每天的生活里,是真真切切让普通人受益的“科学设计”。为啥说它是人类社会迄今为止最科学的制度?不是空喊口号,而是实实在在解决问题、贴合人心。首先, ... 科技之最01-25
-
科技的光,该照向何方? 写字楼里的送餐机器人正灵活地穿梭于电梯间,它们精准地停在每个工位前,完成一次毫无差错的配送。不远处,无人快递车在马路上规整地行驶,车厢里装着人们网购的各式商品。这一幕幕看似科幻的场景,如今却已成为我们 ... 科技之最01-25
-
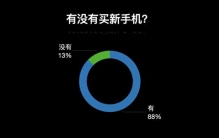
雷科技编辑部2025:没人追新iPhone,但买了这些「真香」产品 春节即将到来,在这种辞旧迎新的时候,也是大家做年度复盘的最好时机。过去一个月里,雷科技已经发布了多个企业、行业的年度回顾和盘点。而作为年度盘点中的保留环节,接下来该盘点一下雷科技编辑部小伙伴今年买了些 ... 科技之最01-25
-
麦克斯韦方程组与电磁学:科学史上最伟大的公式之一 大家好,我是你的科学史探索者。今天我们要穿越时空,走进一段令人震撼的科学革命——麦克斯韦方程组的诞生,以及它如何彻底改变了我们对电磁世界的认知。这不仅仅是一组数学公式,更是一扇开启现代科技大门的钥匙, ... 科技之最01-25
-
中国科技正高速崛起,但距离全球顶尖还有多远? 在过去的几个月里,从中兴芯片制造突破到核聚变研发进展,中国科技一次次被推到风口浪尖。网络上常见两种声音:有人大肆称中国已令世界震惊,也有人悲观地认为中国仍旧脆弱。这种截然相反的观点,恰好暴露了大众对科 ... 科技之最01-24
-
交付破10万!智己LS6铸就科技平权标杆,LS8携热望而来 今日,上汽集团旗下高端电动品牌智己汽车传来重磅消息:旗下热销车型LS6累计交付量已成功突破10万辆大关。与此同时,品牌宣布即将正式官宣新一代旗舰车型——智己LS8,引发市场高度期待。LS6:10万车主认证,科技平 ... 科技之最01-24
-
一核五阶多维:让县域孩子的科学梦想破土而出 “为什么有的树叶在秋天会变黄而有的树叶不会变黄呢?”“为什么机器人能够听懂我们说的话呢?”“为什么同一种蔬菜在太空里种植和在地球上种植的结果不一样呢?”孩子们心中这些天马行空的疑问,正是科学教育最珍贵 ... 科技之最01-24
-
中国量子科技有多强?若继续打破西方垄断,将引起新一轮科技革命 前言量子科技,这个看似神秘的技术领域,在悄悄改变着世界的格局。十年前,中国在很多高科技领域还是个跟跑者,现在在量子科技这个前沿赛道上跑到了第一梯队。从“九章”量子计算机的问世,到星地量子通信的实现,再 ... 科技之最01-23
-
从装订学徒到电学之父:法拉第与改变世界的科学传奇 在科学史上,很少有人能像迈克尔·法拉第那样,以卑微的出身铸就辉煌的成就,用纯粹的热爱改写人类文明的轨迹。这位19世纪最伟大的物理学家、化学家,从一名普通的装订学徒起步,凭借对科学的执着追求与惊人天赋,发 ... 科技之最01-23
-
牛顿与爱因斯坦:站在物理学巅峰的巨人,改变人类历史的科学传奇 大家好!今天我们要探讨的是两位站在物理学巅峰、用智慧重塑世界的伟大科学家——牛顿和爱因斯坦。他们不仅仅是科学的探索者,更是人类认知的开拓者。他们的科学成果,深刻地揭示了世界的本源、现在和未来,成为人类 ... 科技之最01-23
相关文章
- 牛顿与爱因斯坦:站在物理学巅峰的巨人,改变人类历史的科学传奇
- 【好评中国】河声丨科技“丰收年”里,读懂中国,看见未来
- 红魔11 Air上手:无孔直屏+实体风扇,游戏手机卷向新赛道
- 一克千金!造火箭卫星离不开的“黑科技”,曾被日美垄断
- 以系统思维加快高水平科技自立自强
- 投票啦!科研最美瞬间等你来选!
- 中国科学院院士、西湖大学校长施一公到访重庆一中,为师生讲述“生命科学之美”
- 华天科技:全球第六的练成与代价——买来的技术与长不出的能力
- 壁仞科技崛起背后:“第一猎头”全球挖人
- 中国制造重机枪时,因一个低级的错误,却意外造就世界之最
- 4000年前的史前黑科技:龙山文化三大未解之谜,至今无人能复刻
- 为何西方都认为中国最强盛的并非汉唐而是拥有先进科技的此朝
- 解码“生命科学之美”!施一公院士走进重庆八中
- 欧拉:数学史上的百科全书,开启现代科学的黄金钥匙
- xAI“格罗克”深度伪造色情图像诉讼是美国科技伦理最棘手的问题
- HBM风口下,通富微电、华天科技、长电科技 深科技谁最值得关注?
- 珠海神话:中国最牛民办大学之一的大学(珠海科技学院)如何炼成
- 2025:中国科技引爆全球!12个月改写人类命运,未来已来
- 甘肃酒泉,到底骗了多少人?居然拥有 10 个 “世界之最”!
- 中国量子异军突起,或将引爆新一轮科技革命
热门阅读
-
万事胜意不能乱说的原因?告诉你万事胜意该对谁说 12-09
-
科威特第纳尔为什么那么值钱?比美元值钱的货币盘点 12-22
-
撕心裂肺十大催泪情歌,10首哭到崩溃的歌曲 12-24
-
不敢公布马航真实原因,内幕曝光简直太惊人! 12-25
-
陈百强什么原因怎么走的,陈百强85事件是什么 01-05
-
麻将公式一定要背下来,麻将手气背转运小妙招 01-19