当今最复杂的椭圆曲线找到了！29个独立有理点打破18年记录

选自quantamagazine

作者：Joseph Howlett

机器之心编译

机器之心编辑部

又是计算机帮了忙。

对现代密码学稍有了解的人都必定听过椭圆曲线的赫赫威名，但椭圆曲线本身依然还存在很多悬而未决的问题。今天，量子杂志作者 Joseph Howlett 介绍了这方面的一项打破 18 年记录的新突破：找到了一条迄今为止有理点模式最复杂的椭圆曲线。

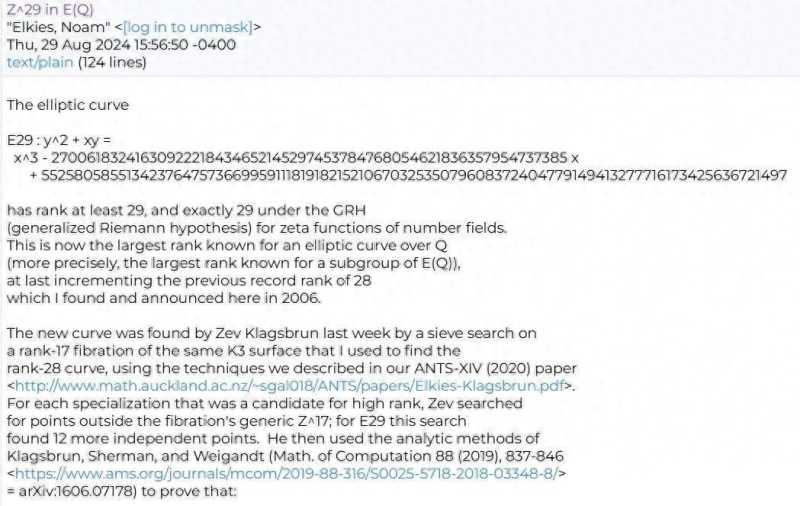
宣布发现这条突破性曲线的邮件截图

今年 8 月，两位数学家发现了一条打破记录的怪异曲线。在此过程中，他们触及了一个仍待解决的重大难题 —— 其涉及到数学领域一类最古老、最基础的方程。

椭圆曲线至少可以追溯到古希腊，是许多研究领域的核心。它们具有丰富的底层结构，数学家们用它开发了许多强大的技术和理论。在 1994 年 Andrew Wiles 著名的费马大定理（是当时数论领域最重要的未解问题之一）证明中，椭圆曲线就发挥了重要作用。椭圆曲线对现代密码学也至关重要。

即便如此，对于椭圆曲线的某些最基本的问题，数学家们仍在寻找答案。举个例子，他们常通过研究椭圆曲线上的特殊「有理点（rational point）」来描述其特征。在一条给定的曲线上，这些点会形成清晰且有意义的模式。但我们目前尚不清楚这些模式的多样性和复杂程度是否有极限。

通过解答这个问题，可让数学家们理解数量巨大且种类繁多的椭圆曲线世界 —— 这个世界中的许多曲线都仍未得到探索。因此，数学家们开始探索这个世界的外围，寻找模式越来越奇怪的异常曲线。这个过程很艰辛，并且既需要创造力，也需要复杂的计算机程序。

现在，哈佛大学的 Noam Elkies 和加利福尼亚州拉霍亚通信研究中心的 Zev Klagsbrun 这两位数学家发现了一条至今为止有理点模式最复杂的椭圆曲线，打破了 18 年前的记录。

「这个阻碍能否打破是一个重大问题。」克罗地亚萨格勒布大学的 Andrej Dujella 说，「对于我们所有研究和关注椭圆曲线的人来说，这是一个非常令人兴奋的结果。」

寻找有理性

椭圆曲线的形式为 y² = x³ + Ax + B，其中， A 和 B 是有理数，它们看起来是这样的：

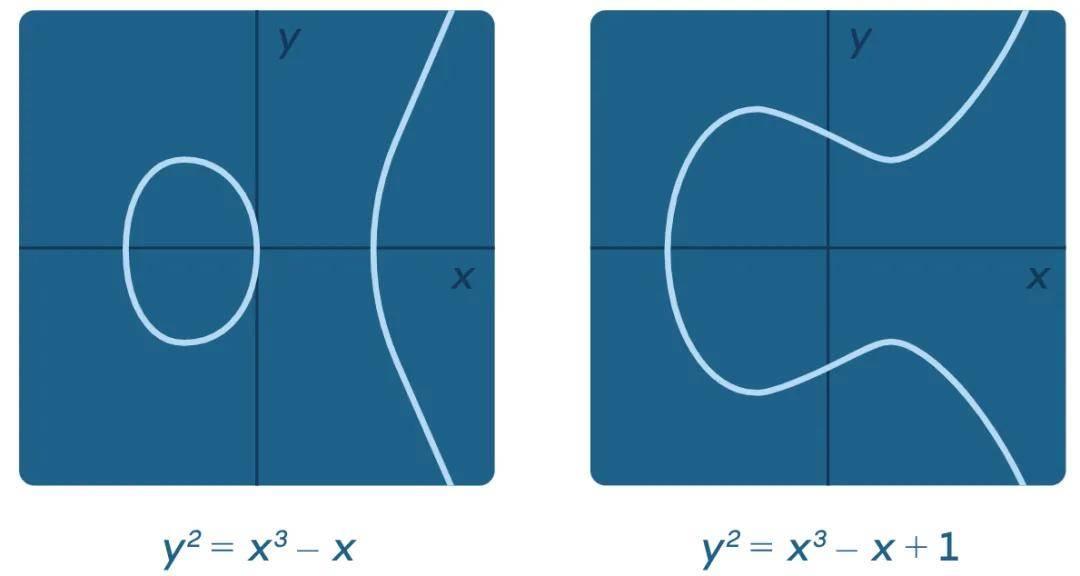
在椭圆曲线的研究中，数学家们特别关注其有理解 —— 即曲线上 x 值和 y 值都是有理数的点。俄亥俄州立大学的 Jennifer Park 表示：这实际上是人类数学历史上最古老的问题之一。

虽然找到简单类型方程的有理解相对直接，但椭圆曲线是真正存在许多未解问题的第一类方程，布朗大学的 Joseph Silverman 说道。「这仅仅是一个三次方程的两个变量，就已经足够复杂了。」

为了掌握椭圆曲线的有理解，数学家们常常依赖于曲线的秩，这是一个衡量曲线上有理点密集程度的数字。秩为 0 的椭圆曲线只有有限数量的有理点。秩为 1 的椭圆曲线拥有无限多的有理点，但所有这些点都按照一种简单的模式排列，这意味着如果你知道其中一个点，就可以遵循一个众所周知的程序来找到其余的点。

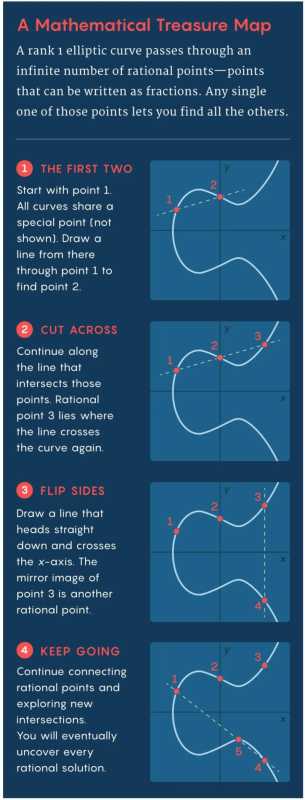
高秩的椭圆曲线同样拥有无限多的有理点，但这些点之间的关系更加复杂。例如，如果你知道一个秩为 2 的椭圆曲线的有理解，你可以使用在秩为 1 情况下相同的程序来找到一整个家族的有理点。但是，这条曲线还有第二个家族的有理点。这意味着这些有理点分布在曲线上以更复杂的方式，形成多个线性独立的族群。

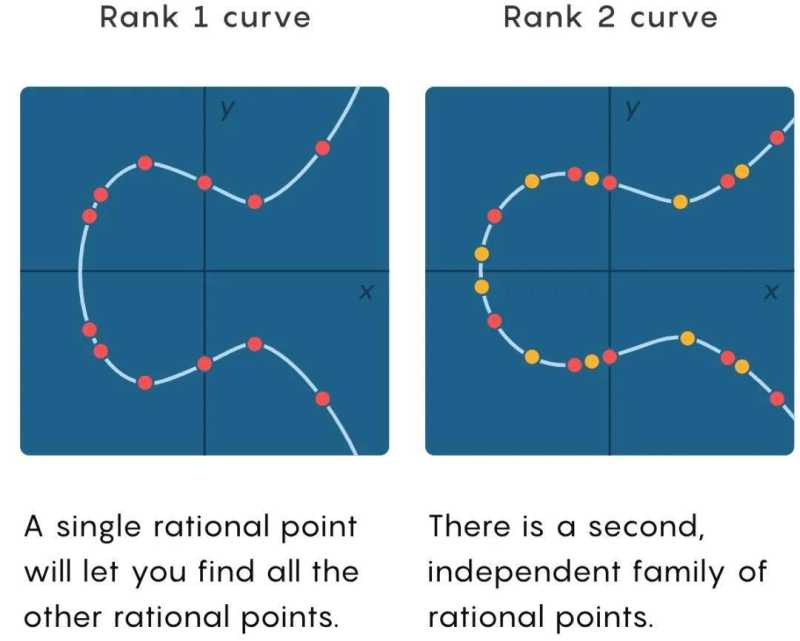
椭圆曲线的秩告诉数学家们需要多少个独立的点，即来自不同家族的点 —— 以定义其有理解的集合。秩越高，曲线上的有理点就越丰富。秩为 2 和秩为 3 的曲线都有无限多的有理解，但秩为 3 的曲线包含来自额外家族的有理点，这意味着在平均情况下，一定长度的曲线将包含更多这样的点。

几乎所有的椭圆曲线都已知是秩为 0 或秩为 1。但仍然有无限多的异常情况具有更高的秩 —— 并且这些曲线极其难以找到。

因此，数学家们不确定秩是否有限制。在相当长的一段时间里，大多数专家认为理论上可以构造任何秩的曲线。最近的证据表明情况并非如此。由于没有确凿的证明，数学家们只能就椭圆曲线的真实本质进行辩论，这正说明了这些方程还有很多未知之处。

更大的一盘棋

Elkies，一位杰出的数论学家。在 2000 年代中期，他正在专注于看似无关的研究，称为 K3 曲面。为了理解它们，Elkies 将它们切割并观察各个部分。

想象一开始有一个简单的表面，一个平面。你可以将其切割成无限多的直线，这些直线并排放置。根据你切割的方式，最终得到的线条将由不同的方程定义。

同样地，有更复杂的、曲线的表面，当切割时，会产生无限多的椭圆曲线。自 1950 年代以来，数学家们一直在使用这些表面来找寻高秩椭圆曲线。

Noam Elkies

Elkies 意识到 K3 曲面足够奇特，可以让他接触到更奇特的曲线。2006 年，他以正确的方式对一个特定的 K3 曲面进行了切片，并在切片中发现了一条椭圆曲线，他可以证明该曲线的秩至少为 28，打破了之前 24 的记录。这对椭圆曲线专家来说是一个激动人心的时刻，他们相信接下来可能会出现一大批打破纪录的人。

然而，之后并无大的突破。Elkies 的记录保持了将近二十年 —— 这与自 1970 年代以来数学家们相对稳定的刷新记录的速度形成了明显的背离。

这或许是一种迹象，表明秩毕竟可能是有限的，或者，这仅仅反映了这一研究确实很难？

在 2006 年 Elkies 公布他的发现之际，Zev Klagsbrun 正就读于纽约皇后学院本科。他的一位教授，曾在 80 年代和 Elkies 比过同一场高中数学竞赛。在办公时间，Zev 被告知了这个破纪录的曲线的新消息。

这是 Zev 首次对寻找有理点产生兴趣。

Zev Klagsbrun

Zev 对此很感兴趣。多年后，他重新审视了 Elkies 的结果，证明了一个猜想是正确的 ——Elkies 的曲线的秩恰好是 28。

因此，当 Zev 在 2019 年的一个会议上遇到 Elkies 时，他说服了 Elkies 重新开始寻找新的曲线。

「我当时说，嘿，我愿意写代码，和我一起继续破解椭圆曲线的秘密吧！」Zev 说。

在 Elkies 同意之后，他们重新审视了十八年前 Elkies 研究过的 K3 曲面。当时，Elkies 通过切片，得到了结论：这些曲线的秩至少为 17，但他的目标是超越 24 的记录。

由于无法直接计算每一条曲线的秩，Elkies 筛选出在数百万条曲线中最可能具有异常高秩的候选，再手动计算这些曲线的秩，直到最终找到了那条秩为 28 的曲线。

Klagsbrun 提供了一个更快的计算方法，把 Elkies 能处理的数百万条，扩展到了数十万亿条。

这次更广泛的搜索，从旧的曲线堆中发现了许多不寻常特性的曲线，但它们都没有打破 28 秩的记录。两人决定继续前进。

四年过去了。然后就到了几个月前，Elkies 和 Klagsbrun 在一次会议上再次相遇，并开始交谈。

他们开始以不同的方式对 K3 曲面进行切片，得到了一个可以研究的新曲线堆。但是，切片方法有好几百种，而大多数切片方法似乎都不太可能得到他们想要的曲线。

然后，他们完全偶然地发现了一种切片方法，就像 Elkies 之前的那种方法一样，可以得到一个曲线堆，并且保证其中所有曲线的秩都至少为 17。与其他方法相比，这种方法似乎更可能挖到宝。果然，使用 Klagsbrun 更强大的计算技术，他们在这个曲线堆中发现了一条秩至少为 29 的椭圆曲线。这条椭圆曲线具有迄今为止发现过的最复杂的有理解集：需要至少 29 个独立点才能描述其特征。

这条曲线的方程如果写成 y² = x³ + Ax + B 的形式，则 A 和 B 的值都有 60 个数字那么长。Elkies 和 Klagsbrun 找到的 29 个独立的有理解涉及的数同样巨大。

29 个独立点的 x 轴坐标

抓住极限

对于椭圆曲线的秩是否有上限的问题，这个结果并未将其彻底解决。「现在我们已经找到了这一条秩更高的曲线，那就有理由去希望」存在具有任意高的秩的曲线，Klagsbrun 说，「另一方面，老天，找到这一条就耗费了大量功夫。很显然想要找到更高秩的样本，还需要一些新思路。」

不过如果能将他和 Elkies 的努力推进得足够远，也许能够扭转局面。他们需要找到一个无限的曲线堆，保证其秩至少为 22（而不是 17，这是他们迄今为止所能做到的最好结果）。如果存在这样一个堆，那就会与「秩存在有限上限」的已有最有力证据相矛盾。

不管怎样，这条秩 29 曲线的发现都拓展了这个未知领域的边界。正如生物学家试图通过研究生活在极端环境中的生物来了解生命一样，通过绘制椭圆曲线世界的极端边缘，数学家也可以获得很大收获。

原文链接：

https://www.quantamagazine.org/new-elliptic-curve-breaks-18-year-old-record-20241111/

https://listserv.nodak.edu/cgi-bin/wa.exe?A2=NMBRTHRY;b9d018b1.2409&FT=&P=&H=&S=b