人类数学史上出现的三次危机，最后一次危机至今仍未解决！

我们从小就会接触到数学，甚至两三岁的时候爸妈就会教我们数数，简单的加减法。人类也是如此，人类诞生之后，就开始了对数学的研究。

据研究考证，人类最早的计数方式是结绳计数，这也是人类对数学研究的雏形，简单粗暴，但也很明了。

古人类对数学的研究都怀有一种朴素的观念，在数学体现出来的就是朴素的整数观，认为整数可以代表世界上的所有事物，这也符合人们的日常生活经验，毕竟人们每天看到的都是可具体化的整数，而分数也是广义上的整数。

但是，随着人类对数学的深入研究，一个颠覆性的变革开始了，这个变革源于人们发现了直角三角形的斜边长度与直角边的关系，也就是后来的勾股定理。

人们发现，如果直角边的长度为1，那么斜边的长度就显得很诡异，长度为根号2。但是当人们计算根号2时，一下变得狂躁起来。

人们发现根号2太长了，不管计算多长时间，都计算不完。而根号2也是人类发现的第一个无理数。

无理数的发现彻底颠覆了人们对数学的朴素认知，彻底颠覆了整数代表的和谐和自然美。人们并不想承认根号2的存在，但现实就摆在那里，于是人们开始对无理数进行了深入研究。

这个时候，一个著名的悖论，芝诺悖论就出现了。

话说有一只乌龟和你赛跑，你的速度是乌龟的十倍。由于乌龟跑得很慢，公平起见，让乌龟在你前方10米的地方开始跑。

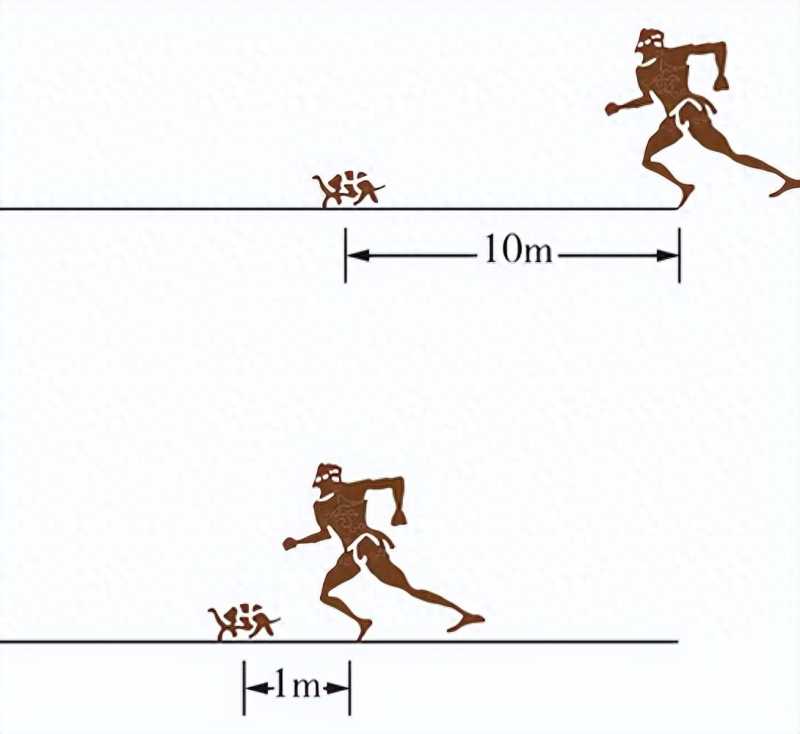
如此一来，当你跑10米的时候，正好跑到乌龟之前的出发点，这时候乌龟跑1米。而当你跑1米的时候，乌龟跑了0.1米。

如此这样下去，你永远在乌龟后面，因为你到达的地点一直都在乌龟之前到达的地点。

但是我们都知道结果不是那样的，你很快就会超过乌龟。为何会出现如此大相径庭的结果？

芝诺悖论让人们不得不重新思考无穷的概念，人们当然知道芝诺悖论肯定在某个地方存在着弊端。

把一段线段进行无限分割势必需要无穷多的时间，但是我们的时间并不是无限的，而是有限的，也就不可能在有限的时间里做无穷多的事情，如此一来就不会陷入总是追赶乌龟跑过的路程。

这种对无穷的理解让当时的人们化解了第一次数学危机，一直持续了上千年，直到牛顿和莱布尼茨的出现。

两人一起发现了微积分，这里就不讨论到底是谁先发现的了。微积分的出现，让当时的人类可以更好地解决很多看似不可能解决的问题，比如说测量弯曲图形的面积，还有曲线的长度。

微积分的思想是建立在无限细分后再整合的思想上，这种思想里总是有无限逼近零的概念。无限小和零到底有什么关系？当时的人们弄不清楚，很多时候甚至直接把无限小等同于零，但并不知道其中的数学含义。

举个例子，一条斜线，我们该如何计算曲线上某个点的切线斜率呢？可以这样做，在这个点旁边设定一个无限小的直角三角形，它的斜边就是这个点的切线斜率。

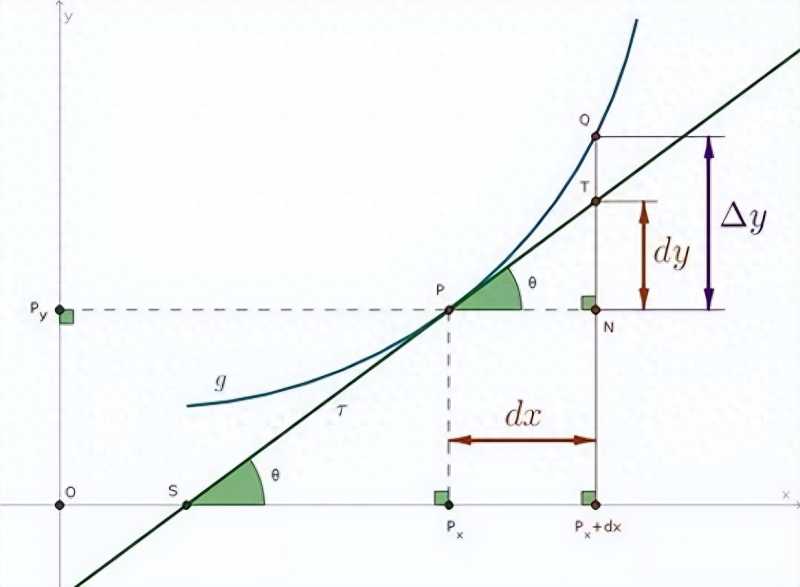
但是当时的人们心里面总是有一道过不去的坎，总是认为不管直角三角形有多小，它的斜边也不可能完全等同于点的切线斜率。

这就出现了第二次数学危机，这次危机简单来讲就是人们一直认定0.999......一定比1小，事实上，两者是相等的。说白了，无限逼近一个数，结果就是那个数。

第二次数学危机，归根结底在于人们对微积分的理解还存在偏差。

第三次数学危机的出现并不是某个数的危机，而是人们对集合论的质疑。“罗素悖论”更能让我们理解这种质疑到底来自何处。

罗素悖论讲述的是这样的故事。一个非常牛的理发师在门口打广告：能给所有不能给自己理发的人理发！

细心的你可能会发现问题了。这个理发师可以给自己理发吗？无论可以还是不可以，最终都会导致矛盾。

因为如果理发师可以给自己理发，就不是“给不能给自己理发的人理发了”。如果不能给自己理发，又打自己的脸了！

这就像我们经常所说的“上帝悖论”一样，上帝无所不能，但他能否创造一个他自己不能搬动的石头呢？无论能或者不能，结果都是矛盾的。

在很多人眼里，“罗素悖论”看起来更像是诡辩，是对集合定义的诡辩，但至今为止仍旧没有死能完美解释这一悖论。

从哲学上来讲，罗素悖论更像是本体论，更像是唯心与唯物的对抗。

如果你是唯心主义者，你会认为世界都是假象，都是你幻想出来的。那么问题就来了。“你”本人的概念也是你的意识幻想出来的吗？如果是，“你”对你自己的质疑也是意识幻想出来的假象吗？

如果仍然是，那么“你对“你质疑自己的思想”的质疑”还是幻想出来的假象吗？

如果一直都是，你这个意识本体到底在哪里？还存在吗？如果你的意识存在，就无法解释刚才的矛盾。如果不存在，那么你就不是唯心的，就矛盾了。

通俗来讲，“罗素悖论”总是一开始就把自己放在事物的外面，然后换一个角度又把自己放在事物当中，问题就在于自己到底在哪里？外面还是里面？