到底是谁最早作出正十七边形的设计,十七边形

是高斯

还是约翰尼斯·厄钦格

前几天，超模君po了各种动图让大家了解不一样的数学（传送门），最后一张高斯尺规作图正17边形引起了各位模友的激烈讨论：

有模友说看不明白

有好奇他是怎么想出来的

有说正17边形高斯并没有画出来

甚至在超模君讲根号2的故事时（传送门），也留言说希望讲讲正17边形的故事。

既然如此，那今天超模君就将这些问题一并解决了吧。。

---------------------------------------------

相传，在1776年的一天，德国哥廷根大学，19岁的高斯像往常一样，吃完晚饭，开始做导师每天单独布置给他的数学题。

然后，轻松完成了老师布置的前两道题。

第三道题是另外写在一张小纸条上的，是要求只用圆规和一把没有刻度的直尺作出正17边形。

高斯并没有在意，像做前两道题一样开始做起来。。。

虽然感觉这道题做起来有点吃力，他还是坚持想要做出来。

他拿起圆规和直尺，在草稿纸上写写画画，也尝试着用一些超常规的思路去解这道题。

经过通宵的演算，他终于解出了这道难题。

当导师得知自己的学生竟然一个晚上就解开了这道有两千多年历史的数学悬案时，万分惊讶，连连夸赞高斯是天才。

原来，导师也一直想解开这道难题。那天，他只是不小心才将写有这道题目的纸条交给了高斯。

多年以后，当高斯回忆起这一幕时，总是说：如果有人告诉我，这是一道有两千多年历史的数学难题，我不可能在一个晚上解决它。

这可能就是人们常说的无知者无畏吧。

------------------------------------------------

通过这个故事，大家都认为正17边形最早是高斯画出来的了。

然而，关于尺规作图正17边形的故事还有另一个版本。

事实上，高斯在哥廷根大学就读时，在一次偶然的阅读中，他知道了用直尺和圆规作出圆内接正七边形的难题。这使他非常着迷，并决心要功克它。他首先查找出前人的作图方法，仔细研究他们失败的原因，通过半年多的努力，他终于作出了正七边形；接着，正九、正十一、正十三边形都被他一一克服。没多久，正十七边形也被他功克。

有人认为：高斯本人并不会作正17边形，他只是证明了正17边形可以用尺规作出来。

而第一个画出正17边形的是约翰尼斯·厄钦格，他于1825年发表了正17边形的尺规作图方法。

到底哪个说法是正确的呢？

超模君经过查阅资料，了解到这些：

1796年3月30日，高斯开始在笔记中记录他的科学发现。

1898年在高斯的孙子保留的遗物中偶然发现了这本笔记，高斯称之为“日志录圆的分割定律，如何以几何方法将圆分成十七等份。

也即是说，高斯于1796年证明怎样的正多边形可以用尺规作出来，并发表了研究成果，轰动整个学术界。

就在同年3月30日，他在笔记中记下了正17边形的作法，然而并没有发表（确实，相对于证明怎样的正多边形可以用尺规作出来，这一点就显得微不足道了）。

而在1825年，约翰尼斯·厄钦格第一次公开发表正17边形尺规作图法。

到了1898年，人们在整理高斯遗物的时候，才发现高斯笔记中的正17边形作法。

由此，超模君得出结论：高斯并非不会作正17边形（记到笔记中，没发表），而约翰尼斯·厄钦格确实是最早给出正17边形作法的人。

那高斯怎么就知道正十七边形是可以用尺规作出来的呢？

因为他数学厉害啊！（小天：请不要敷衍我们。。。）

首先，高斯知道：如果一个正多边形内角的三角函数能用含有基本算术（加减乘除）和平方根的公式表达出来，那这个正多边形就能用尺规作出来。

尺规作图等价于只使用圆和直线的交点作图，直线的表达式是二元一次方程，圆的表达式是二元二次方程，所以只用到了加减乘除和平方根。

而后来他又证明了：只要正多边形的边数n是费马素数，那么就能用这样的公式表达。

当时已知的前五个费马素数是3、5、17、257和65537，因此高斯等于一举证明了这五种正多边形都是尺规可作的。

不过，正三边形和正五边形人们早就会作了，而正257边形什么的作起来又太麻烦，所以最后正17边形就成了最出名的。（因为是高斯啊。。）

1832年，F.J.Richelot出版了一本用尺规制作正257边形的小册子，后来一位Hermes教授花了十年的青春画出了正65537边形。

那么正17边形所对应的三角函数是这样的呢？

有兴趣的可以看一下如下证明：

设正17边形的一条边对应的中心角为a，则17a = 2π，即16a = 2π - a。故sin(16a) = -sin(a)

而sin(16a) = 2sin(8a)cos(8a) = 4sin(4a)cos(4a)cos(8a) = 16sin(a)cos(a)cos(2a)cos(4a)cos(8a)故 -sin(a) = 16sin(a)cos(a)cos(2a)cos(4a)cos(8a)

因 sin(a) 不为0故16cos(a)cos(2a)cos(4a)cos(8a) = -1

用余弦函数积化和差公式进行迭代，有：2(cos(a) cos(2a) ... cos(8a)) = -1

令 x = cos(a) cos(2a) cos(4a) cos(8a)

y = cos(3a) cos(5a) cos(6a) cos(7a)

则：x y = -1/2

xy = (cos(a) cos(2a) cos(4a) cos(8a))(cos(3a) cos(5a) cos(6a) cos(7a))

对xy进行展开, 积化和差, 再利用周期性合并同类项，有：

xy = (1/2)(4cos(a) 4cos(2a) ... 4cos(8a) )

即xy = -1

联立方程组，得：

x = (-1 √17) / 4

y = (-1 - √17) / 4

再设x1 = cos(a) cos(4a)， x2 = cos(2a) cos(8a)

y1 = cos(3a) cos(5a)，y2 = cos(6a) cos(7a)

积化和差，再利用 2(cos(a) cos(2a) ... cos(8a)) = -1 有：

x1x2 = -1/4

y1y2 = -1/4

故同法可解x1，x2，y1，y2：

x1 = (-1 √17 √2 * √(17 - √17)) / 8

x2 = (-1 √17 - √2 * √(17 - √17)) / 8

y1 = (-1 - √17 √2 * √(17 √17)) / 8

y2 = (-1 - √17 - √2 * √(17 √17)) / 8

最后，由cos(a) cos(4a) = x1

2cos(a)cos(4a) = y1 可求cos(a)之表达式：

它是由整数经过加、减、乘、除、开平方构成的。

故正17边形可用尺规作出。

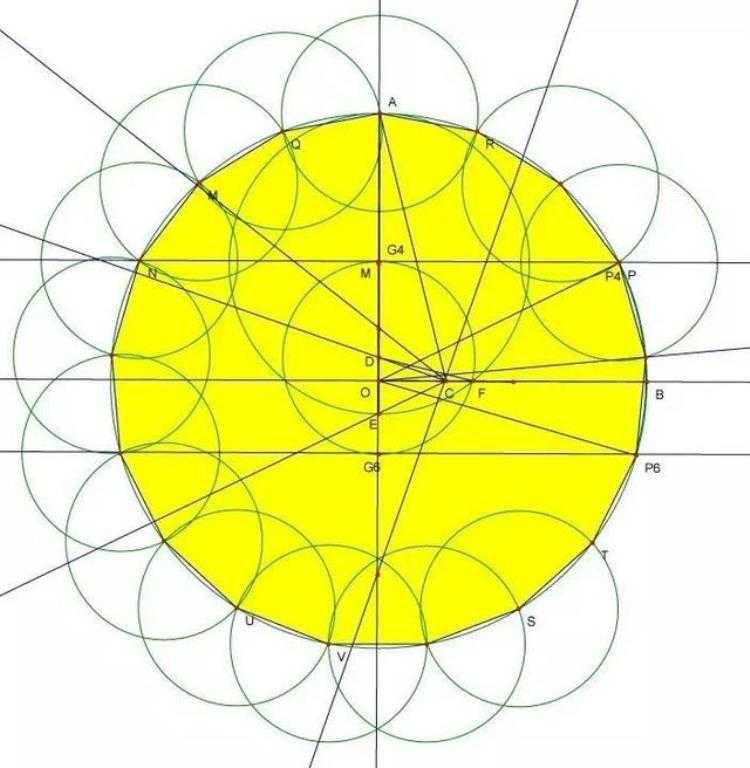
还有，很多人说这个动图太快了，看不懂（只觉得好厉害），那现在超模君来分享一下现代数学家H.W.Richmond的画法吧！（这个真的可以自己动手画的哦）

第一步：

给一圆O，作两垂直的直径OA、OB，

作C点使OC＝1/4OB，

作D点使∠OCD＝1/4∠OCA

作AO延长线上E点使得∠DCE＝45°

第二步：

作AE中点M，并以M为圆心作一圆过A点，

此圆交OB于F点，再以D为圆心，作一圆

过F点，此圆交直线OA于G4和G6两点。

第三步：

过G4作OA垂直线交圆O于P4，

过G6作OA垂直线交圆O于P6，

则以圆O为基准圆，A为正十七边形之第一顶点，

P4为第四顶点，P6为第六顶点。

以1/2弧P4P6为半径，即可在此圆上截出正十七边形的所有顶点。

via：星云风暴

本文由超级数学建模编辑整理

部分资料来源于网络

转载请在公众号中，回复“转载”

-----这里是数学思维的聚集地------

“超级数学建模”（微信号supermodeling），每天学一点小知识，轻松了解各种思维，做个好玩的理性派。30万数学精英都在关注！

商务合作请加微信zwz2434